shivaseの日記

SIer→Web→教師→SIer→ベンチャー(SRE)と異色な人生を歩んでいるエンジニアの日記

Machine Learning Week1 - Model and Cost Function

Coursera Coursera-Machine Learning

Machine Learning Week1 - Introduction の続き

このレッスンは、線形回帰の中でもシンプルな一変数による線形回帰(Linear Regression with One Variable)がターゲット

「住宅の広さ(x)から、家賃(y)を予測する」時のように、「一つの変数xから、全体の結果を予測する」 ような二次関数の導き方を学習する。 = 単回帰(Univariate linear regression)

univariate linear regression graph

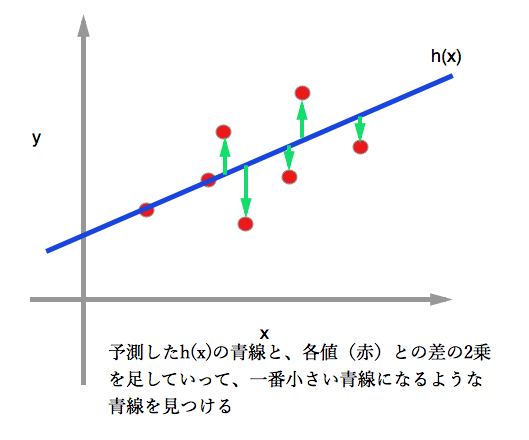
データが上図の赤点だとすると、二乗誤差目的関数というのを使って、妥当な二次関数（青線）が評価できるようになる。

表記（シンボル)

今後の数式で出てくる表記が何を示すのか理解しておく

  • {m} : 訓練サンプルの数(Number of training examples)
  • {x's} : 入力変数(input variable / features)
  • {y's} : 出力変数(output variable / target variable)
  • {(x,y)} : 一件の訓練サンプル(one training example)
  • {(x^{(i)}, y^{(i)})} : i番目の訓練サンプル
  • {h} : 予測(hypothesis)関数
    -> hは入力変数を出力変数へ対応させる関数 (h maps from x's to y's)

予測関数

予測関数とは上図でいう青線にあたるもの。以下のような数式で表す

{ \displaystyle
h_\theta(x) = \theta_0 + \theta_1x
} 
↓　短縮系
 {
h(x)
}

パッと見難しいけど、ようは二次関数(y=ax + b)の形。 {\theta_0}は初期値(b)のことで、{\theta_1}はxの傾き具合(a)のこと。

この {h(x)}の最適解を求める関数を目的関数（cost function)と呼び、このレッスンで扱う 二乗誤差目的関数もその一つ。

二乗誤差目的関数

cost function graph

数式にするとこれ

{ \displaystyle
J(\theta_0,\theta_1) = \frac{1}{2m} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)})^2
}

二乗誤差目的関数は、この {J(\theta_0,\theta_1)} が最小の値になるようなパラメータ（ {\theta_0,\theta_1})を見つけていく目的関数。＝＞ {minimize J(\theta_0,\theta_1)}

※ 二乗誤差 => 図乗の緑で示した差(誤差)を二乗しているから

Ng「なぜ二乗するのでしょう？」

Ng「これが妥当な選択(reasonal choice)だから」

(´・ω・｀)なんじゃそりゃ…

残差を最小にするような最小二乗法で求めた推定値が、不偏で最小の分散を持つことを保証する定理である

ガウス＝マルコフの定理 - Wikipedia

参考：最小二乗法は、なぜ「二乗」なのでしょうか？ - 数学 | 教えて！goo

{\theta_0 = 0}だった場合の最適解

{h_\theta(x) = 0 + \theta_1x}の場合は、 {\theta_1}と二乗誤差の関係を図にすると以下のようになる。

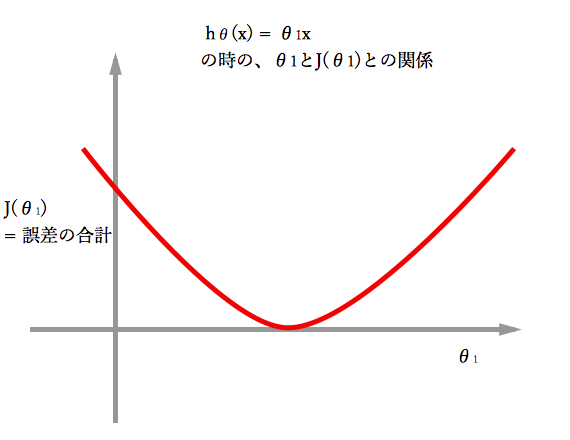J(θ)とθの関係グラフ つまり二乗誤差目的関数はある一点の最適解だけがある状態となる。（シンプル

{\theta_0 \neq 0}だった場合の最適解

パラメータが {\theta_0}と {\theta_1}になるので、 {\theta_0}及び {\theta_1}と二乗誤差の関係はボウル型の三次元となる. この3次元での最小値は、次で学習する最急降下法（Gradient Descent)を使って求めていく

参考にしたサイト

目的関数 : はじめての最適化（第1回）

【スポンサーリンク】